Résumé !

Again one of those posts.
I learned that a political friend, a very good one from far right white suppremacy groups has a cancer. The Guy is just three years younger than me.
Obviously, he is triple dosed.
Yes, you could Say "well, Fuck him", as you know , i'm unvaxed myself.
But still, it's a fucking tragedy what is happening, and how the conspiracy theorists are always right.

Thanks to the number station radio team and to sebastien who gave a full explanation.

The sequence is at most 11 numbers long, e.g. [6, -9, 6, 6, -10, 6, -10, 6, 6, -9, 6]
There is no 12 numbers long sequence that satisfies the required properties
For a 12 numbers long sequence, the sum of eight consecutive numbers being positive implies
a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7 > 0  (1)
a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8 > 0  (2)
a2 + a3 + a4 + a5 + a6 + a7 + a8 + a9 > 0  (3)
a3 + a4 + a5 + a6 + a7 + a8 + a9 + a10 > 0  (4)
a4 + a5 + a6 + a7 + a8 + a9 + a10 + a11 > 0  (5)
And the sum of 5 consecutive numbers implies
a0 + a1 + a2 + a3 + a4 < 0  (6)
a1 + a2 + a3 + a4 + a5 < 0  (7)
a2 + a3 + a4 + a5 + a6 < 0  (8)
a3 + a4 + a5 + a6 + a7 < 0  (9)
a4 + a5 + a6 + a7 + a8 < 0  (10)
a5 + a6 + a7 + a8 + a9 < 0  (11)
a6 + a7 + a8 + a9 + a10 < 0  (12)
a7 + a8 + a9 + a10 + a11 < 0  (13)
Anyways substracting the previous inequalities gives
a0 + a1 + a2 > 0  (1-9)
a1 + a2 + a3 > 0  (2-10)
a2 + a3 + a4 > 0  (3-11)
a3 + a4 + a5 > 0  (4-12)
a4 + a5 + a6 > 0  (5-13)
a5 + a6 + a7 > 0  (1-6)
a6 + a7 + a8 > 0  (2-7)
a7 + a8 + a9 > 0  (3-8)
a8 + a9 + a10 > 0  (4-9)
a9 + a10 + a11 > 0  (5-10)
Subtracting these from 1 to 5 again gives a[n] + a[n+1] < 0
Subtracting these from 1 to 5 again gives a[n] + a[n+1] < 0

And there's no sequence that long where the sum of 2 consecutive numbers is negative while the sum of 3 consecutive numbers is positive
(Basically a0 + a1 + a2 > 0 and a0 + a1 < 0 implies a2 > 0, a1 + a2 + a3 > 0 and a2 + a3 > 0 implies a1 > 0, which implies a1 + a2 > 0)
So that means there's no 12 numbers long sequence satisfying these properties.
And any longer sequence would necessarily include a 12 number long subsequence which would also have to match these properties

The last nerd challenge is over .
The sadistic mathematicians are satisfied. It was so hard, that only three persons got it right. Even the koreans didn't get it.
Congratulations to Heckler, Sebastien and Unit 731.
And now the answer.

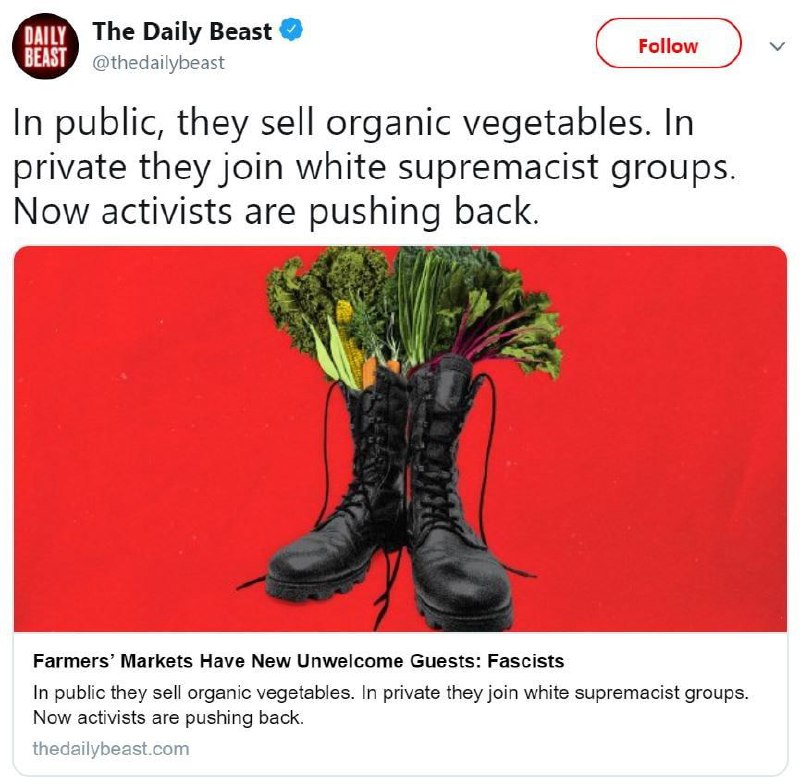
Neo fasc....farmers ( 2 parts )

You want to create a civil War in a Telegram chat ?
Simple.
just ask if it is better to have the penis circumcised or not.