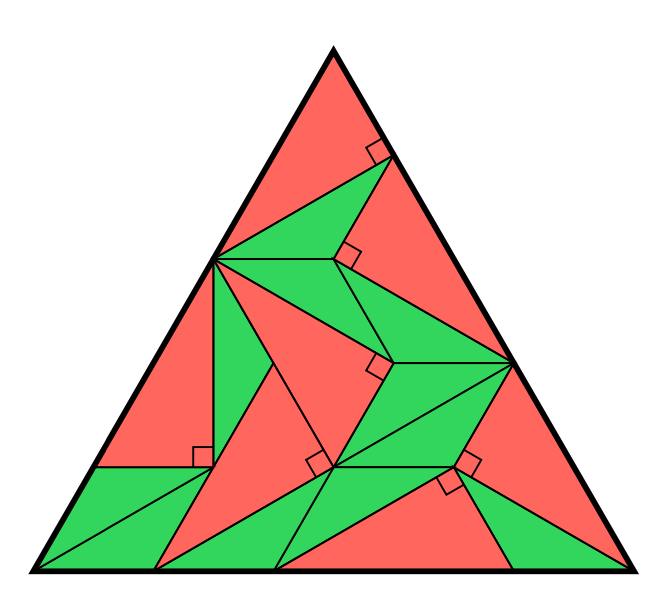
правильный треугольник сложен из одинаковых прямоугольных красных треугольников и одинаковых равнобедренных зеленых треугольников

во сколько раз площадь большого треугольника больше площади зеленого?

// доступная начинающим задача М.Евдокимова с проходившего вчера Турнира Ломоносова

поздравляем Пьера Делиня с 80-летием!

Замощения плоскости — мозаики — позволяют увидеть равносоставленность равновеликих многоугольников.

Эта идея у нас уже встречалась, например, в одном из доказательств теоремы Пифагора: один слой — это замощение плоскости квадратами двух разных размеров, второй слой — квадратная сетка.

Сегодняшняя модель — разрезание квадрата и равновеликого правильного восьмиугольника на одинаковые части https://etudes.ru/models/square-octagon/ . Его даёт такая мозаика https://t.me/EtudesRu/762 : первый слой — снова замощение плоскости квадратами двух разных размеров, второй слой — сетка из маленьких квадратов первого разбиения и правильных восьмиугольников.

Это и ещё одно разрезание квадрата и правильного восьмиугольника встречается в персидской рукописи неизвестного автора, найденной в 1970 году в национальной библиотеке Франции (Anonymous Compendium / Paris, Bibliothèque nationale de France, Ms. Persan) и датируемой примерно XIV веком.

Интересующимся восточными орнаментами всячески рекомендуем страницу Андрея Ивановича Щетникова — удивительного человека, в частности, известного как автора образовательного проекта GetAClass.

Можно ещё всё это сделать прямо в трёхмерном пространстве — благо, что третье (перпендикулярное плоскости орбиты) направление задаётся вектором момента импульса. И тогда новый сохраняющийся вектор «виртуального» момента тоже будет там же — и вроде бы (я не доводил счёт до конца, но ничего другого получиться не должно) это должен быть вектор Лапласа—Рунге—Ленца, разве что, делённый на квадрат массы (и может быть, ещё на какую-нибудь константу?).

\sqrt{r^2 + (vt)^2} = r \sqrt{1 + (vt/r)^2} = r + (1/2) (vt)^2 / r + o(t^2),
так что вторая производная равна

v^2/r = (vr)^2 / r^3.

Числитель — (vr)^2 — это квадрат углового момента. Так что он вдоль орбиты всегда один и тот же!
А знаменатель r^3 — как раз и соответствует закону всемирного тяготения: куб, как и раньше. Так что, если взять константу
l = (vr)^2/ (GM),
то для разницы (r-l) будет
(r-l)’’ = r’’ = hr + (vr)^2 / r^3
= - GM r / r^3 + (vr)^2 / r^3
= - GM / r^3 * (r- l)
= h (r-l).

Так что трёхмерный вектор R = (x,y,r-l) подчиняется центральному закону
R’’ = h R, h = -GM/r^3.

Ура — теорема доказана!

В исходной плоскости (x,y) действует радиальная сила, поэтому вектор ускорения (x’’,y’’) пропорционален радиус-вектору r=(x,y) — с коэффициентом
h=-GM/r^3
(в знаменателе куб, потому что нам нужен единичный вектор в нужном направлении, а это отношение r/r, вот ещё одна степень r в знаменателе и появляется).

Поэтому
x’’ = hx
y’’ = hy.

Если бы радиус r был линейной комбинацией x и y, то для его второй производной было бы такое же соотношение, и центр даже двигать бы не пришлось. Но — давайте зафиксируем единичный вектор b=(b_x,b_y), в начальный момент направленный по радиусу, и рассмотрим линейную функцию (r,b) = b_x x + b_y y.

Эта линейная функция в первом порядке совпадает с радиусом r, а на радиальном луче совпадает с ним совсем. Так что их вторые производные будут отличаться только за счёт вклада от перпендикулярного радиусу движения точки :

r’’= b_x x’’ + b_y y’’ + (вклад от перпендикулярного движения)
= hr + (вклад от перпендикулярного движения)

Если v — это нормальная к радиусу компонента скорости, то этот вклад это
v^2 * (вторую производную радиуса при движении по касательной к окружности),
или, что то же самое, вторая производная при движении по касательной к окружности со скоростью v.
И вот сейчас момент импульса (секториальная скорость) и вылезет — ведь ровно за него/неё перпендикулярная радиусу скорость v и отвечает!

https://www.shawprize.org/laureates/2024-mathematical-sciences/

The Shaw Prize in Mathematical Sciences 2024 is awarded to Peter Sarnak, Gopal Prasad Professor, School of Mathematics, Institute for Advanced Study and Eugene Higgins Professor of Mathematics, Princeton University, USA, for his development of the arithmetic theory of thin groups and the affine sieve, by bringing together number theory, analysis, combinatorics, dynamics, geometry and spectral theory.

Ответ на этот вопрос даёт формула Лефшеца.

Выглядит она так. Раз отображение f действует на многообразии M — оно действует и на всех k-мерных гомологиях
H_k(M,\R)
(которые мы будем рассматривать с вещественными коэффициентами, так что это векторное пространство).

Слово «гомологии» заслуживает отдельного комментария, но если вы с ними не сталкивались — давайте временно ограничимся тем, что это какие-то векторные пространства, сопоставленные многообразию, и измеряющие, насколько в нём есть что-то нетривиальное «в размерности k». Например, у сферы с g ручками нуль-мерные гомологии это одномерное пространство (порождённое «точкой»), двумерные гомологии это тоже одномерное пространство (порождённое «всей поверхностью»), а вот одномерные гомологии это пространство размерности 2g (порождённые обходами «вдоль» и «поперёк» каждой из ручек — или, что то же самое, «параллелями» и «меридианами» каждого из g торов, как связную сумму которых можно представить поверхность).

Так вот — отображение f действует на каждом из пространств k-мерных гомологий как линейное преобразование. А с линейным преобразованием много чего связано — в частности, можно рассмотреть след
tr (f_* , H_k(M,\R))

Давайте посмотрим на знакопеременную сумму таких следов. Оказывается, это и есть ответ!

Теорема (формула Лефшеца).
\sum_{f(p)=p} ind_f(p) = \sum_{k=0}^n tr(f_* , H_k(M,\R)).

То есть — сумма индексов неподвижных точек отображения определяется тем, как именно оно «перекручивает» многообразие. Красиво, правда?

Пример. Возьмём векторное поле v и «проедем» вдоль него небольшое время t_0 — получив диффеоморфизм f. Его неподвижные точки это в точности особые точки v (если время было достаточно малым, чтобы ни одну периодическую орбиту мы не успели полностью проехать). И индексы у них для отображения и для векторного поля одни и те же. Так что по теореме Пуанкаре–Хопфа сумма их индексов равна эйлеровой характеристике.

С другой стороны, заметим, что f гомотопно тождественному отображению (что f в тождественное отображение «можно перетянуть»). Действительно, достаточно рассмотреть семейство сдвигов вдоль того же векторного поля v за разные времена t. При t=0 это тождественное отображение, а при t=t_0 — наше f. Вот мы непрерывно и перетянули f в id.

А гомотопные отображения одинаково действуют на гомологиях. Так что для такого f его действие на каждых гомологиях просто тождественно, и значит, каждый след это просто размерность соответствующего пространства гомологий. А знакопеременная сумма размерностей пространств гомологий действительно равна эйлеровой характеристике!

P.S. Несколько ссылок про гомологии:
- курс В. А. Васильева «Гомологии, наборы плоскостей и формула включений-исключений» в ЛШСМ-2011: https://www.mathnet.ru/present3568
- книга В. В. Прасолова «Элементы теории гомологий», МЦНМО, 2006 https://old.mccme.ru/free-books/prasolov/homol.pdf
- курс Г. Ю. Паниной в ЛШСМ-2023: https://old.mccme.ru//dubna//2023/courses/panina.html

Wikipedia

Число Лефшеца

Число Лефшеца — определённая целочисленная характеристика отображения топологического пространства в себя.

Продолжим? Представим себе, что у нас векторное поле v задано не на плоскости, а на какой-то ориентированной поверхности S — сфере, торе, кренделе, и т. д. То есть нам дана поверхность S, и в каждой точке p\in S задан вектор v(p), касательный к S в этой точке.…

какими формулами задаются «Вавилонские» итерации?

если одна сторона прямоугольника площади 2 равна x, то вторая равна 2/x

дальше мы заменяем x на среднее арифметическое двух сторон, x→x/2+1/x (и прямоугольники становятся все ближе к квадратам, а x все ближе к √2)

сравним это с методом Ньютона: чтобы найти корень уравнения f(x_0)=0, мы начинаем с какого-то x и представляем себе, что f примерно линейная — если f(x+t)≈f(x)+tf'(x), то f≈0 при t=-f(x)/f'(x), т.е. новое приближение получается заменой x→x-f(x)/f'(x)

в частности, для функции x²-2 мы получаем те же самые итерации: x-(x²-2)/(2x)=x/2+1/x