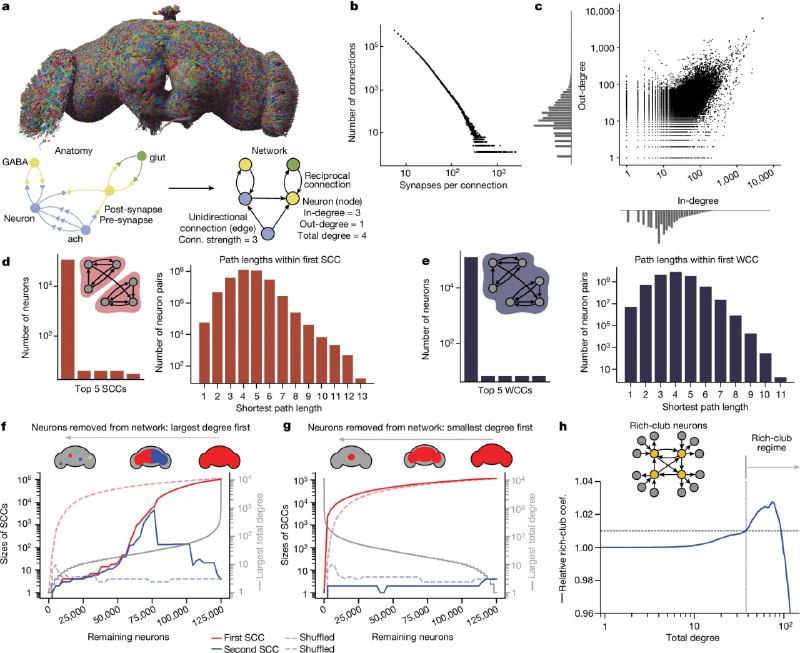
Вчера свершилось великое — наконец доделали мозг взрослой дрозофилы

“We observed 2,700,513 such connections between 134,181 identified neurons” — в 20 раз больше, чем у личинки дрозофилы, которую год назад выкладывали

Как сейчас часто бывает, статьи выходят пачкой, поэтому в том же номере Nature есть сразу же статья с анализом опубликованного коннектома:

"...we computed the prevalence of two- and three-node motifs, examined their strengths, related this information to both neurotransmitter composition and cell type annotations4,5, and compared these metrics with wiring diagrams of other animals. We found that the network of the fly brain displays rich-club organization, with a large population (30% of the connectome) of highly connected neurons. We identified subsets of rich-club neurons that may serve as integrators or broadcasters of signals. Finally, we examined subnetworks based on 78 anatomically defined brain regions or neuropils. These data products are shared within the FlyWire Codex and should serve as a foundation for models and experiments exploring the relationship between neural activity and anatomical structure."

А также статья с подробной клеточной аннотацией всех 140 000 нейронов

(картинка из статьи с анализом)

Начинаем чтение Modern Algebra and the Rise of Mathematical Structures, Corry

Возвращаемся к разговору о структурах в математике, и теперь предлагаю вместе с Корри проследить историю алгебраических структур. В первой части обсудим, что такое структурный подход на примере развития теории идеалов от Дедекинда до Нётер. Во второй части посмотрим на три наиболее влиятельные попытки сформулировать теорию математических структур. Начнём с менее известной работы Ойстина Оре, в которой алгебраическая структура определялась на основе идей теории решёток. Дальше обсудим Бурбаки. Вероятно, большинство ассоциирует идею структур в математике именно с их работой. Закончим, конечно же, теорией категорий — самым подробным и успешным примером теории, которая позволяет систематически анализировать различные структуры.

Встречаемся на нашем дискорд-сервере в субботу, 24 августа, 18:00 по Москве, прочитать "Introduction: Structures In Mathematics".

Книга в первом комменте.
Сервер: https://discord.gg/Pa4az2e7MC

Предыдущий пост "От моноидов к ∞-монадам" в виде pdf.

Статья Gunnar Carlsson и Facundo Mémoli

QUANTAL COMPONENTS OF THE END-PLATE POTENTIAL (1954)

В современных вычислительной биологии модели зачастую идут параллельно с реальностью и не проверяются экспериментально должным образом: модель считается самодостаточным результатом. Данная работа, ставшая уже классической (>2000 цитат), демонстрирует то, как моделирование и эксперимент могут дополнять друг друга, в результате позволяя ответить на фундаментальные вопросы.

Del Castillo и Bernard Katz (нобелевский лауреат 1970-го) экспериментировали на лягушках, записывая токи с концевых мышечных пластинок и заметили, что если мотонейрон, аксон которого образовывал синапс с концевой пластинкой мышцы, спайковал, заливая всё ацетилхолином, то на пластинке регистрировался сильный деполяризующий отклик — потенциал концевой пластинки (end-plate potential или EPP) амплитудой в 20 mV (заряд смещался с -75mV до -55mV), однако, даже в отсутствии спайка на аксоне мотонейрона, на концевой пластинке регистрировались слабые потенциалы в 0.5 mV, которые было решено назвать миниатюрными потенциалами концевой пластинки (miniature end-plate potential или mEPP). Было предположено, что EPP = сумма большого числа mEPP случившихся в коротком временном интервале, где каждый mEPP – ответ на некоторый квант ацетилхолина, высвобождаемого пресинапсом. Стоит понимать, что про везикулы и синаптическую передачу тогда ничего толком не знали, поэтому квант – по факту одна условная везикула, случайно или неслучайно излившая содержимое в синаптическую щель. Тогда усредненная амплитуда EPP должна быть равна: V_e = npq, где n – число доступных квантов ацетилхолина в пресинапсе, а p – средняя вероятность высвобождения кванта (везикулы) в синаптическую щель, а q – амплитуда mEPP (в оригинале quantal amplitude). Собственно, вся статья 1954-го года посвящена проверке этой модели экспериментально. С этой целью ученые искусственно варьировали синаптическую проводимость, понижая концентрацию кальция (который нужен для высвобождения везикул, как мы сейчас знаем) и повышая магния, тем самым получив ответный EPP на спайк моторного нейрона амплитудой всего в несколько mV – несколько квантов или mEPP в рамках гипотезы. Если предложенная модель корректна, тогда среднее количество везикул-квантов высвобождаемых за каждый EPP должно быть равно m=np. При этом, условно зная (провидение), что число n везикул в пресинапсе большое, а вероятность экзоцитоза p маленькая, они предположили, что число везикул высвобождаемых в синаптическую щель должно аппроксимироваться Пуассоновским распределением, таким образом вероятность высвобождения x везикул-квантов в конкретном испытании равна P(x) = (m^x / x!) exp(-m). Это даёт два возможных способа получения числа m. Во-первых, это средняя амплитуда регистрируемого EPP, деленного на амплитуду q или mEPP. Во-вторых, экспериментальные условия приводили к тому, что регистрировалось множество нулевых EPP – когда никакого отклика на стимуляцию моторного нейрона в концевой пластинке не регистрировалось вследствие крайне малого значения p, что аналогично P(0) = exp(-m), а P(0) экспериментально можно получить как отношения числа неудач к общему числу испытаний. Если модель корректна, тогда оба этих пути оценки числа m должны давать идентичный результат m = mean(V_EPP)/q = ln(число испытаний/число неудач). Собственно, собрав данные они это и увидели. Такой квантовый анализ до сих пор используется в экспериментальной науке для анализа синаптических ответов, например, для локализации пре- и постсинаптических изменений связанных с LTP и LTD. И да, результаты этой работы во многом легли в основу современного знания о ВПСП и ТПСП в ЦНС, сама природа mEPP как бы намекает на сущностное родство.