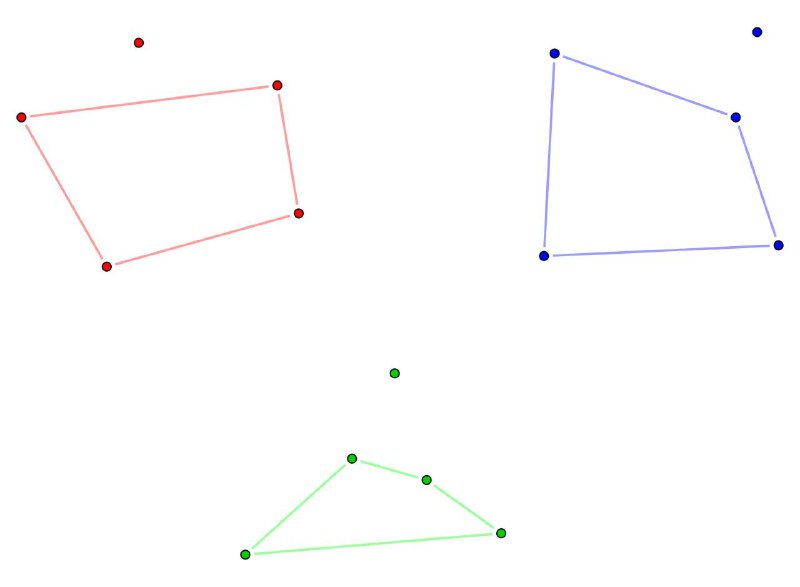
Есть задача, которая называется «Задача со счастливым концом» или "Happy ending problem". Это утверждение про то, что из любых пяти точек общего положения можно будет найти четыре, чтобы построить выпуклый четырехугольник. Общение положение у точек — это когда никакие три не на одной прямой. И у этого утверждения есть еще и попытка обобщения о том, сколько именно точек достаточно в общем случае, чтобы мочь найти там n-угольник. Есть надежда, что это 2^(n-2)+1.

Я сначала подумала, что кто-то очень обрадовался этому факту, что хотя бы для четырехугольника удалось доказать, фух, слава те господи. И поэтому она так называется. А на деле это реально Happy Ending problem!

В 1933 Эстер Кляйн сидела на скамейке (или нет) со своими друзьями-математиками и предложила им придумать такое общее расположение у точек, что не удастся найти на них выпуклый четырехугольник. Эрдёш и Джордж Секереш (ну и фамилия, да? Жесть. На англ. вообще пишется как Szekeres) заинтересовались и стали заниматься этим вопросом. Кстати, Джордж, кажется, вовсе не Джордж, а Дьёрдь, то есть и с фамилией, и с именем всё сложно у него. Но в общем, они тогда взялись за этот вопрос, а Секереш стал тусить с Кляйн.

Годы спустя, когда Секереш и Кляйн поженились, Эрдёш так назвал эту проблему, потому что счёл, что это был момент, который позволил их отношениям завязаться.

Кстати, Эрдёш и Секереш потом еще занимались более общим вот этим вопросом.

А Эстер и Дж... Дьёрдь жили долго (каждый прожил больше девяноста лет) и умерли в один день (28 августа 2005 года). Реально хеппи ендинг, представляете.

<..> говоря о математических способностях, Колмогоров объявил, что для занятий математикой на не слишком высоком уровне — во всяком случае, на уровне, достаточном для обучения на мехмате — не требуется никакой специальной одарённости, что это доступно всякому нормальному человеку, но что, конечно, некоторые элементарные способности всё же надо иметь, в частности, надо обладать тем, что называется пространственным воображением. И каждый в состоянии сам проверить наличие у себя этих простейших необходимых способностей с помощью несложных тестов. Слушателям был предложен один из таких тестов, как раз на наличие пространственного воображения: понять, каким образом при пересечении куба плоскостью может получиться шестиугольник. Это не очень сложно, сказал Колмогоров, и каждый претендующий на то, чтобы выбрать математику своей профессией, должен уметь представить себе соответствующий чертёж. А уж кто не умеет, тому разумно поискать другую профессию. Тут Колмогоров дал всем минуты три для самостоятельных попыток, после чего нарисовал на доске куб и стал пересекать его плоскостью. Как он ни старался, шестиугольник у него не получался. Он слегка разозлился, стёр куб и перешёл к следующей теме.

(c)

Геометрия вызывала у индийцев меньший интерес. Доказательства теорем состояли из чертежа и слова «смотри».

Ну вообще, считаю, нормальный подход.

В древнеегипетском папирусе нцатого века ДО н.э. какие-то умники уже находили сумму геометрической прогрессии.

И смешно записывали дроби. У них были почти исключительно аликвотные дроби (когда в числителе единица, внизу натуральное число). Кроме специальных символов для 2/3 и 3/4.

3/4 похожа на плачущий кровью глаз.