Привет, товарищи-статистики!

Я, наконец-то, дописал статью про мета-анализ, о котором менее строго писал ранее в канале.
https://habr.com/ru/companies/X5Tech/articles/862202/

Что важно:
- в статье есть обещанный разбор тестирования зависимых гипотез.
- формализованный вывод метода Фишера через преобразование случайной величины
- рассмотрены еще ряд статистик для независимых тестов

Постарался как и всегда дать это максимально просто, надеюсь, получилось.

Статья большая, не меньше, чем я написал про Mann-Whitney, но должна быть максимально исчерпывающей.

P.S. Аналитик из Gett - это Дима, @DVars, спасибо и тебе за мотивацию написать эту простыню)

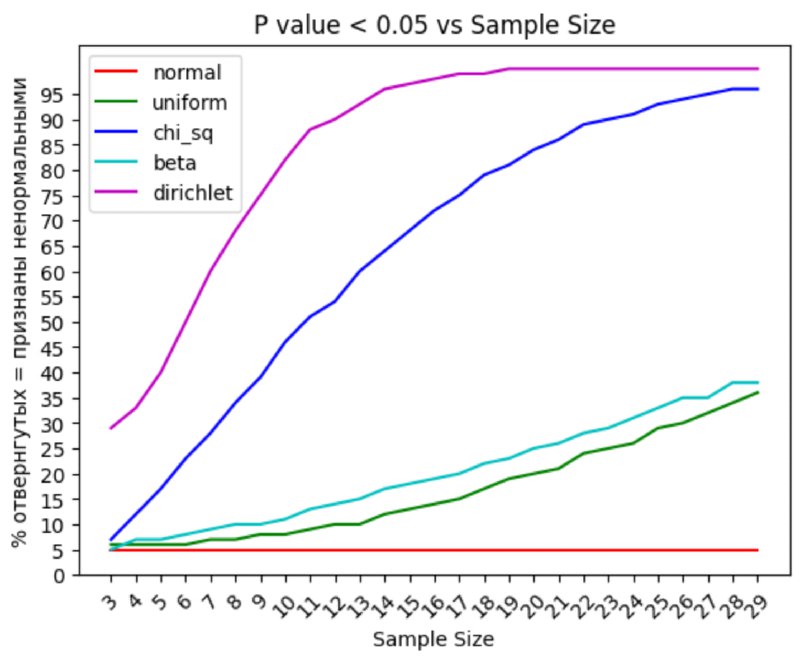
Привет, товарищи-статистики!
Или, как мы дошутились с коллегой Валерой, товарищи, - представили субкультуры,- абешники и абешницы.

В посте выше я вскользь написал, что мне в принципе понятна мотивация делать ошибочных ход: проверять тестом на нормальность выборку для t-test'a. Но думаю, было бы полезно объяснить почему это ход даже не столько ошибочный, сколько бессмысленный.

Продолжение бессмыслицы.

• неожиданным образом пришлось откомментировать пост глубоко уважаемого мною Филлипа Ульянкина в попытке уменьшить разночтения от моих слов, слов коллег из X5 и Филлипа в голове тех, кто только трогает статистику

Привет, товарищи статистики!

Все собирался пост написать, да не мог. Но в моем случае часто работает "спросили интересный вопрос" -> "родился пост". В общем, благодаря беседе в чате Юры Борзило и вопросу Сергея в частности (спасибо!) этот пост и появился (но немного с другой постановкой вопроса):

"Допустим запустили мы АБ, получили p-value 0.051 (уровень значимости alpha = 0.05), что делать?"

Привет, товарищи статистики.

Хотел поделится впечатлениям от докладов, которые хотел посетить и посетил на Aha.

1) "Causal Impact. Как делать эксперименты там, где нет классический AB-тестов. Теория, практика и "подводные камни" метода"
Очень надеялся, что подача будет иная. Так и получилось. Лучший доклад из всех, что был на конференции. Конкретный, последовательный. Вообще, очень классно, что презентация сама по себе содержательна: так и надо делать.

Дмитрий наглядно погружает в метод, библиотеку, ряд проблем и далее дает рекомендации, как проблемы эти преодолеть. Опять-таки, наглядно (я такое очень люблю и сам стараюсь практиковать)

Выделю несколько моментов, не по порядку:
- Отдавать предпочтение классическим A/B-тестам (sic!)
- Оценивать уровень стат. значимости и мощность через Монте-Карло (так вы поймете не просто их значения, но и надо ли вам тюнить модель прогноза или нет)
- Критерии качества модели прогноза и указания на работу с гиперпараметрами (были ссылки на видео и на статью)
- Поиск ковариат (независимая предсказательная/контрольная переменная)

Очень хороший доклад как опорный материал к Causual Impact. В целом, этот метод становится востребованым к пониманию на рынке, рекомендую погрузится. Сделать это можно через следующие материалы (на английском):
- онлайн книга в открытом доступе
- онлайн курс от того автора в открытом доступе

2) Как каузальные графы и линейные модели ответят на все ваши вопросы в A/B-тестах

Докладчиком был Кирилл, глава аналитики в HH (как оказалось, как автора я его знаю - ninja на medium, вот статья, которую я чаще видел в репостах, про требования нормальности в t-test'e). После его выступления я поговорил с ним, чтобы "спрямить" свои впечатления.

Поэтому выскажусь в хорошем ключе так: я согласен с прогнозом Кирилла, который он высказал в личной беседе, что линейные модели это вероятно новый будущий хайп в ближайшие годы. Действительно, A/B через линейки это тот же самый t-test, только сбоку, а если накидывать контрольных переменных, то можно "очищать эффект", и, - чего не было в докладе, - сразу оценивать по сегментам результаты. Все в рамках одного кода.

Но есть проблемы:
- спутывающие переменные (confounding var.), которые влияют и на воздействие и на то, на что целится воздействие
- графах связанности переменных: визуально штуки-то простые, три "шарика" переменных, три связи (цепочка, вилка, ~~бумага~~, коллайдер), а далее их вариации, но сами связи и то, что происходит, если "условится", непривычно воспринимать.
- надо исследовать метрики на предмет того, какой вид группировок "шариков" сходится с реальностью: в общем, вместо дерева метрик предлагается строить графы метрик (что так-то методологически правильнее)

Все это по сути тоже про Causal, но c другой стороны: Сausal Inference
Есть очень хороший видео-материал на английском. Достаточно понятный, но все равно немного привыкнуть к "шарикам" и способу мысли за ними будет нужно.

В общем, штука перспективная, по словам Кирилла уже давно в практике зарубежом (подход вроде выработал гугл в 10-х годах), а до нас катится лишь сейчас, классика. Интересно посмотреть, сбудется ли прогноз. Но в любом случае перейти в свои ноутах на линейные модели в пост-хоке рекомендую.

Если же сделать шаг назад и рассказать о докладе, то, кратко говоря, это был порыв души сообщить не без волнения о том, что возможно грядет ~~покайтесь, грешники~~; учите матчасть. Будет непонятно, но если посмотрите курс выше с пересмотром, то понятно :)

3) - "Влияние сетевого эффекта в AБ-тестах на unit-экономику в ритейле"
Вообще, я бы тут не столько говорил о сетевом эффекте, сколько об учете костов в рамках вашей инициативы, то есть в идеале проводить A/B с учетом затрат по каждой группе (короче, быть в рамках unit-экономики). А то вполне может быть так, что в группе B стат. значимый прирост, но из-за повышенных расходов по экономике убыток.

—
Уже только благодаря этим докладам я рад, что побывал на конфе. Но помимо этого увиделся со многими вживую: рад был всех увидеть и пообщаться!

Вот такие вот впечатления.