Олимпиадная комбинаторика
Чат: https://t.me/+FuCRPdSjWjMyZWU6
⚡️Наука и Факты - порно для мозга
Реклама: @Calve
• Ссылка для друзей: https://t.me/+Dv2bnQYMMxMzZjNi
Биржа: https://telega.in/c/FactTG
Менеджер: @Spiral_Miya
Last updated 1 year, 2 months ago
VISA PARTNER - Крупнейший визовый центр в средней Азии ⭐️
💯 13 лет опыта визовых услуг.
☎️ Офис в Ташкенте: +998974499056
Telegram: @Visa_Partner
Last updated 1 year, 3 months ago
PR/Commercial [email protected] Сотрудничество: @mediapump_M
Твич https://twitch.tv/avilina_melnik
Лайк https://l.likee.video/p/1pJphE
Вк группа https://vk.com/avi.vuni
Заявление в РКН №4931209039
Last updated 1 year ago
набросал вчера относительно длинный черновик поста с примерами того, что хотел бы закодить, но не могу (и почему именно не могу…)
но сегодня что-то посмотрел на один из примеров и решил, что глаза боятся, а… короче, код получился недлинный, но унесу все ж в комментарии
===
интересно считать количество разбиений разных фигур на доминошки
про прямоугольники 2×N и числа Фибоначчи и так все знают
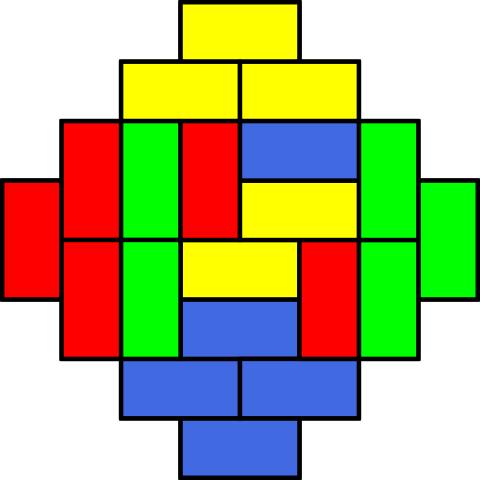
а вот на картинке ацтекский бриллиант порядка 4 — сколькими способами его можно разбить на доминошки? а бриллиант порядка N?
тут общий ответ можно угадать по ответам для небольших N, но перебирать руками тяжеловато (для N=4 вариантов уже больше тысячи), компьютерный эксперимент действительно полезен
про разные способы этот ответ доказывать есть интересная брошюра Е.Смирнова «Три взгляда на ацтекский бриллиант», https://mccme.ru/free-books/dubna/smirnov-aztec.pdf
более естественная, казалось бы, идея — считать замощения обычного квадрата N×N… но там по ответам для маленьких N ничего угадать не возможно
все же перебрал на компутере и замощения квадрата 8×8 — в качестве ответа получилось название лекции С.Смирнова https://www.mathnet.ru/present18250


Опубликуем ещё одну задачу с олимпиады «JetBrains Youth Challenge», автор — К. А. Кноп.
В лиге младших классов она была 8-й из 8, и её решила всего 1 команда. Коллектив жюри ожидал большего количества решений этой задачи?
А оригинальная версия этой задачи была заметно сложнее — причём настолько, что методкомиссия даже не решилась вставлять её в лигу старших классов. Для продвинутых комбинаторов опубликуем и оригинальную формулировку тоже!
Пользуясь случаем, напомню следующую задачу.
У Белочки есть бесконечно много орехов: по одному ореху каждой из
масс 1 г, 2 г, 3 г, \dots. Она взяла n мешков, положила в каждый по
конечному числу орехов, после чего написала на каждом мешке суммарную
массу лежащих в нем орехов.
а) Докажите, что можно было собрать мешки с
такими же массами, использовав не более 4n-3 орехов.
б*) Какова точная оценка на число орехов, которого заведомо достаточно?
Пункт б) я решать не умею.
Прочитал про теорему Дена о разрезании: если прямоугольник можно разрезать на квадраты, то отношение его сторон рационально. Интуитивно это кажется логичным, но доказать не так уж и просто. Обратное утверждение тривиально: если отношение сторон рационально и скажем равно p/q, то увеличив масштаб в q раз, получим прямоугольник с целыми сторонами, который можно разрезать на квадраты 1x1.
Линейная алгебра помогает построить простые и красивые доказательства:
Отношение длин сторон прямоугольника W,H иррационально - это то же, что "W,H линейно независимы как векторы в пространстве R над Q". Это в свою очередь значит, что существует Q-линейная функция f:R->R, так, что f(W) и f(H) - любые удобные нам значения.
Для любой Q-линейной функции f определим f-площадь прямоугольника со сторонами A,B как f(A)*f(B). Тогда легко увидеть, что при разрезании прямоугольника на другие прямоугольники f-площадь целого равна сумме f-площади частей (это очевидно при разрезании одного прямоугольника на два, и к повторению этого можно свести любое разрезание, если сделать из него "сетку", продлив все внутренние линии до краев).
Как ни странно, доказательство почти закончено. f-площадь любого квадрата равна f(A)*f(A), то есть неотрицательна. Отсюда f-площадь любого прямоугольника размером W:H, разрезанного на квадраты, неотрицательна. Но если W/H не рационально, то мы можем выбрать такую f, что f(W)=1, f(H)=-1, и его f-площадь равна -1, это противоречие.
Другое доказательство с помощью линейной алгебры вместо f-площади пользуется тензорным произведением R@R. Если стороны прямоугольника w,h линейно независимы, то {w,h} можно продлить до базиса, и поэтому ясно, что в R@R линейно независимы также векторы w@w, w@h, h@w, h@h. С другой стороны, если прямоугольник разбит на квадраты, то w@h является суммой членов вида a@a (доказательство аналогично примеру с площадью). Это значит, что изоморфизм в R@R, который меняет координаты местами, одновременно переводит w@h в h@w и оставляет неизменным, т.е. w@h = h@w, а это противоречит их независимости.
Еще есть красивое доказательство с помощью гармонических функций на конечных графах (второе в этой заметке). А в древней книжке Яглома "Как разрезать квадрат?" (1968) есть элементарное доказательство через систему уравнений, связывающих длины сторон.
P.S. Вспоминается также замечательная статья "Fourteen proofs of a result about tiling a rectangle", где дается много доказательство похожего, но другого по сути утверждения: что если прямоугольник разрезан на прямоугольники и у каждого внутренного прямоугольника хотя бы одна из сторон - целое число, то и у всего прямоугольника тоже хотя бы одна из сторон целая.
1 и 2 день, решения
⚡️Наука и Факты - порно для мозга
Реклама: @Calve
• Ссылка для друзей: https://t.me/+Dv2bnQYMMxMzZjNi
Биржа: https://telega.in/c/FactTG
Менеджер: @Spiral_Miya
Last updated 1 year, 2 months ago
VISA PARTNER - Крупнейший визовый центр в средней Азии ⭐️
💯 13 лет опыта визовых услуг.
☎️ Офис в Ташкенте: +998974499056
Telegram: @Visa_Partner
Last updated 1 year, 3 months ago
PR/Commercial [email protected] Сотрудничество: @mediapump_M
Твич https://twitch.tv/avilina_melnik
Лайк https://l.likee.video/p/1pJphE
Вк группа https://vk.com/avi.vuni
Заявление в РКН №4931209039
Last updated 1 year ago